Orthogonal projections¶
Highlights In this lecture, we'll show (1) the fundamental theorem of linear algebra:
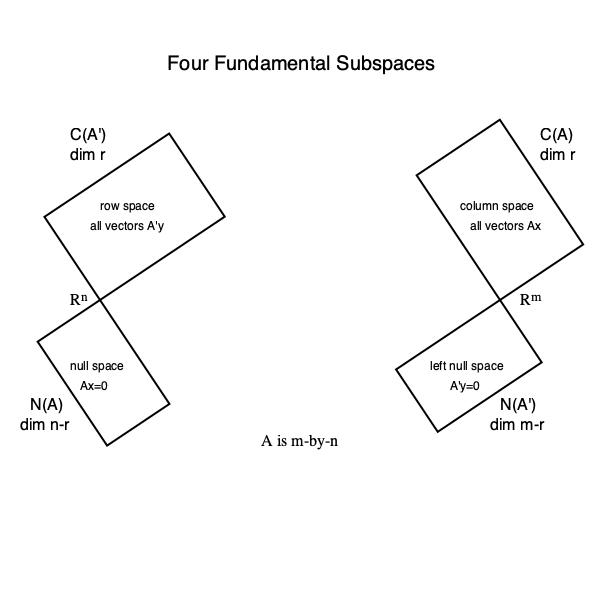
and (2) any symmetric, idempotent matrix $\mathbf{P}$ is the orthogonal projector onto $\mathcal{C}(\mathbf{P})$ (along $\mathcal{C}(\mathbf{P})^\perp = \mathcal{N}(\mathbf{P}')$).
Ortho-complementary subspaces¶
An orthocomplement set of a set $\mathcal{X}$ (not necessarily a subspace) in a vector space $\mathcal{V} \subseteq \mathbb{R}^m$ is defined as $$ \mathcal{X}^\perp = \{ \mathbf{u} \in \mathcal{V}: \langle \mathbf{x}, \mathbf{u} \rangle = 0 \text{ for all } \mathbf{x} \in \mathcal{X}\}. $$ In midterm Q8, we showed that $\mathcal{X}^\perp$ is always a vector space regardless $\mathcal{X}$ is a vector space or not.
TODD: visualize $\mathbb{R}^3 = \text{a plane} \oplus \text{plan}^\perp$.
Direct sum theorem for orthocomplementary subspaces. Let $\mathcal{S}$ be a subspace of a vector space $\mathcal{V}$ with $\text{dim}(\mathcal{V}) = m$. Then the following statements are true.
- $\mathcal{V} = \mathcal{S} + \mathcal{S}^\perp$. That is every vector $\mathbf{y} \in \mathcal{V}$ can be expressed as $\mathbf{y} = \mathbf{u} + \mathbf{v}$, where $\mathbf{u} \in \mathcal{S}$ and $\mathbf{v} \in \mathcal{S}^\perp$.
- $\mathcal{S} \cap \mathcal{S}^\perp = \{\mathbf{0}\}$ (essentially disjoint).
- $\mathcal{V} = \mathcal{S} \oplus \mathcal{S}^\perp$.
$m = \text{dim}(\mathcal{S}) + \text{dim}(\mathcal{S}^\perp)$.
By the uniqueness of decomposition for direct sum, we know the expression of $\mathbf{y} = \mathbf{u} + \mathbf{v}$ is also unique.Proof of 1: Let $\{\mathbf{z}_1, \ldots, \mathbf{z}_r\}$ be an orthonormal basis of $\mathcal{S}$ and extend it to an orthonormal basis $\{\mathbf{z}_1, \ldots, \mathbf{z}_r, \mathbf{z}_{r+1}, \ldots, \mathbf{z}_m\}$ of $\mathcal{V}$. Then any $\mathbf{y} \in \mathcal{V}$ can be expanded as $$ \mathbf{y} = (\alpha_1 \mathbf{z}_1 + \cdots + \alpha_r \mathbf{z}_r) + (\alpha_{r+1} \mathbf{z}_{r+1} + \cdots + \alpha_m \mathbf{z}_m), $$ where the first sum belongs to $\mathcal{S}$ and the second to $\mathcal{S}^\perp$.
Proof of 2: Suppose $\mathbf{x} \in \mathcal{S} \cap \mathcal{S}^\perp$, then $\mathbf{x} \perp \mathbf{x}$, i.e., $\langle \mathbf{x}, \mathbf{x} \rangle = 0$. Therefore $\mathbf{x} = \mathbf{0}$.
Proof of 3: Statement 1 says $\mathcal{V} = \mathcal{S} + \mathcal{S}^\perp$. Statement 2 says $\mathcal{S}$ and $\mathcal{S}^\perp$ are essentially disjoint. Thus $\mathcal{V} = \mathcal{S} \oplus \mathcal{S}^\perp$.
Proof of 4: Follows from essential disjointness between $\mathcal{S}$ and $\mathcal{S}^\perp$.
Some facts (optional):
- For a set $\mathcal{X}$ in a vector space $\mathcal{V}$, $\mathcal{X}^\perp$ is always a subspace, whether or not $\mathcal{X}$ is a subspace.
- If $\mathcal{S}$ is a subspace of $\mathcal{V}$, then $(\mathcal{S}^\perp)^\perp = \mathcal{S}$.
- If $\mathcal{S}_1 \subseteq \mathcal{S}_2$ are subsets of $\mathcal{V}$, then $\mathcal{S}_1^\perp \supseteq \mathcal{S}_2^\perp$.
- If $\mathcal{S}_1 = \mathcal{S}_2$ are two subsets of $\mathcal{V}$, then $\mathcal{S}_1^\perp = \mathcal{S}_2^\perp$.
- If $\mathcal{S}_1$ and $\mathcal{S}_2$ are two subspaces in $\mathcal{V}$, then $(\mathcal{S}_1 + \mathcal{S}_2)^\perp = \mathcal{S}_1^\perp \cap \mathcal{S}_2^\perp$ and $(\mathcal{S}_1 \cap \mathcal{S}_2)^\perp = \mathcal{S}_1^\perp + \mathcal{S}_2^\perp$.
The fundamental theorem of linear algebra¶
Let $\mathbf{A} \in \mathbb{R}^{m \times n}$. Then
- $\mathcal{C}(\mathbf{A})^\perp = \mathcal{N}(\mathbf{A}')$ and $\mathbb{R}^m = \mathcal{C}(\mathbf{A}) \oplus \mathcal{N}(\mathbf{A}')$.
- $\mathcal{C}(\mathbf{A}) = \mathcal{N}(\mathbf{A}')^\perp$.
$\mathcal{N}(\mathbf{A})^\perp = \mathcal{C}(\mathbf{A}')$ and $\mathbb{R}^n = \mathcal{N}(\mathbf{A}) \oplus \mathcal{C}(\mathbf{A}')$.
Proof of 1: To show $\mathcal{C}(\mathbf{A})^\perp = \mathcal{N}(\mathbf{A}')$, \begin{eqnarray*} & & \mathbf{x} \in \mathcal{N}(\mathbf{A}') \\ &\Leftrightarrow& \mathbf{A}' \mathbf{x} = \mathbf{0} \\ &\Leftrightarrow& \mathbf{x} \text{ is orthogonal to columns of } \mathbf{A} \\ &\Leftrightarrow& \mathbf{x} \in \mathcal{C}(\mathbf{A})^\perp. \end{eqnarray*} Then, $\mathbb{R}^m = \mathcal{C}(\mathbf{A}) \oplus \mathcal{C}(\mathbf{A})^\perp = \mathcal{C}(\mathbf{A}) \oplus \mathcal{N}(\mathbf{A}')$.
Proof of 2: Since $\mathcal{C}(\mathbf{A})$ is a subspace, $(\mathcal{C}(\mathbf{A})^\perp)^\perp = \mathcal{N}(\mathbf{A}')^\perp$.
Proof of 3: Applying part 2 to $\mathbf{A}'$, we have $$ \mathcal{C}(\mathbf{A}') = \mathcal{N}((\mathbf{A}')')^\perp = \mathcal{N}(\mathbf{A})^\perp $$ and $$ \mathbb{R}^n = \mathcal{N}(\mathbf{A}) \oplus \mathcal{N}(\mathbf{A})^\perp = \mathcal{N}(\mathbf{A}) \oplus \mathcal{C}(\mathbf{A}'). $$
Orthogonal projections¶
If $\mathcal{S}$ is a subspace of some vector space $\mathcal{V}$ and $\mathbf{y} \in \mathcal{V}$, then the projection of $\mathbf{y}$ into $\mathcal{S}$ along $\mathcal{S}^\perp$ is called the orthogonal projection of $\mathbf{y}$ into $\mathcal{S}$.
The closest point theorem. Let $\mathcal{S}$ be a subspace of some vector space $\mathcal{V}$ and $\mathbf{y} \in \mathcal{V}$. The orthogonal projection of $\mathbf{y}$ into $\mathcal{S}$ is the unique point in $\mathcal{S}$ that is closest to $\mathbf{y}$. In other words, if $\mathbf{u}$ is the orthogonal projection of $\mathbf{y}$ into $\mathcal{S}$, then $$ \|\mathbf{y} - \mathbf{u}\|^2 \le \|\mathbf{y} - \mathbf{w}\|^2 \text{ for all } \mathbf{w} \in \mathcal{S}, $$ with equality holding only when $\mathbf{w} = \mathbf{u}$.
Proof: Picture. \begin{eqnarray*} & & \|\mathbf{y} - \mathbf{w}\|^2 \\ &=& \|\mathbf{y} - \mathbf{u} + \mathbf{u} - \mathbf{w}\|^2 \\ &=& \|\mathbf{y} - \mathbf{u}\|^2 + 2(\mathbf{y} - \mathbf{u})'(\mathbf{u} - \mathbf{w}) + \|\mathbf{u} - \mathbf{w}\|^2 \\ &=& \|\mathbf{y} - \mathbf{u}\|^2 + \|\mathbf{u} - \mathbf{w}\|^2 \\ &\ge& \|\mathbf{y} - \mathbf{u}\|^2. \end{eqnarray*}
Let $\mathbb{R}^n = \mathcal{S} \oplus \mathcal{S}^\perp$. A square matrix $\mathbf{P}_{\mathcal{S}}$ is called the orthogonal porjector into $\mathcal{S}$ if, for every $\mathbf{y} \in \mathbb{R}^n$, $\mathbf{P}_{\mathcal{S}} \mathbf{y}$ is the projection of $\mathbf{y}$ into $\mathcal{S}$ along $\mathcal{S}^\perp$.
Orthogonal projection into a column space¶
- For a matrix $\mathbf{X}$, the orthogonal projector onto $\mathcal{C}(\mathbf{X})$ is written as $\mathbf{P}_{\mathbf{X}}$.
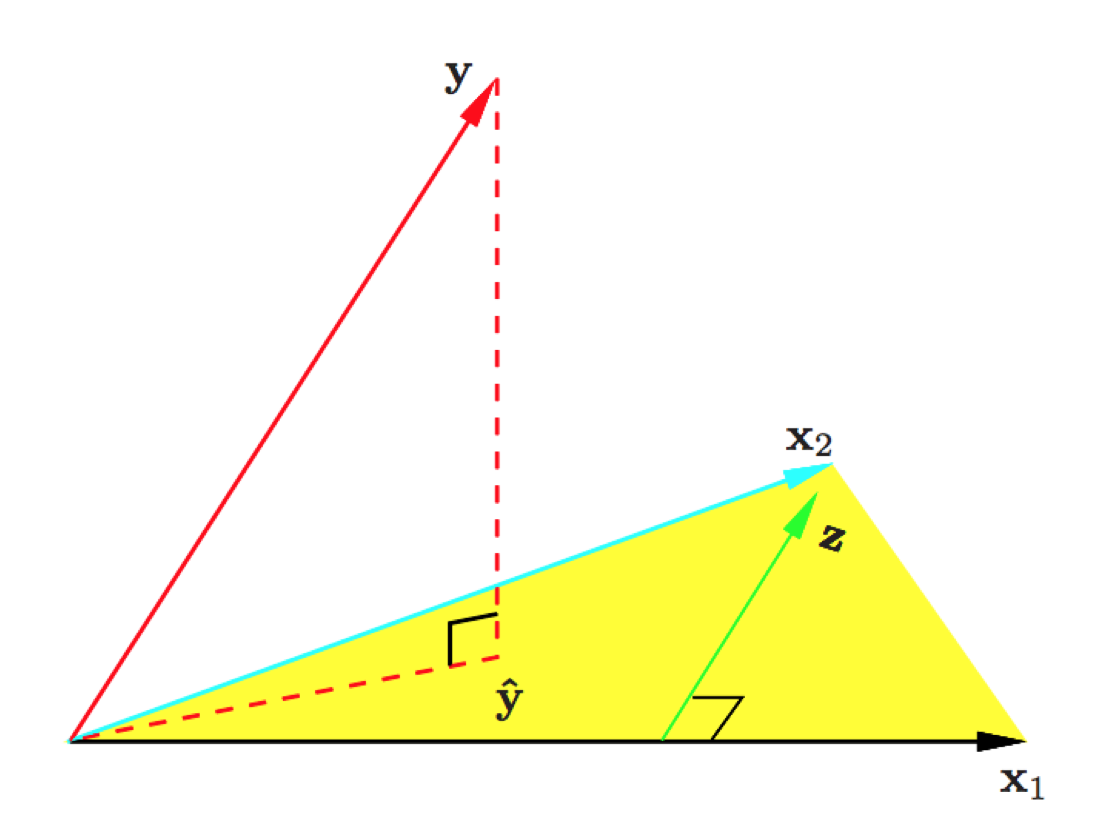
Let $\mathbf{y} \in \mathbb{R}^n$ and $\mathbf{X} \in \mathbb{R}^{n \times p}$.
- The orthogonal projector of $\mathbf{y}$ into $\mathcal{C}(\mathbf{X})$ is given by $\mathbf{u} = \mathbf{X} \boldsymbol{\beta}$, where $\boldsymbol{\beta}$ satisfies the normal equation $$ \mathbf{X}' \mathbf{X} \boldsymbol{\beta} = \mathbf{X}' \mathbf{y}. $$ Normal equation always has solution(s) (why?) and any generalized inverse $(\mathbf{X}'\mathbf{X})^-$ yields a solution $\widehat{\boldsymbol{\beta}} = (\mathbf{X}'\mathbf{X})^- \mathbf{X}' \mathbf{y}$. Therefore, $$ \mathbf{P}_{\mathbf{X}} = \mathbf{X} (\mathbf{X}' \mathbf{X})^- \mathbf{X}'. $$ for any generalized inverse $(\mathbf{X}' \mathbf{X})^-$.
If $\mathbf{X}$ has full column rank, then the orthogonal projector into $\mathcal{C}(\mathbf{X})$ is given by $$ \mathbf{P}_{\mathbf{X}} = \mathbf{X} (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}'. $$
Proof of 1: Since the orthogonal projection of $\mathbf{y}$ into $\mathcal{C}(\mathbf{X})$ lives in $\mathcal{C}(\mathbf{X})$, thus can be written as $\mathbf{u} = \mathbf{X} \boldsymbol{\beta}$ for some $\boldsymbol{\beta} \in \mathbb{R}^p$. Furthermore, $\mathbf{v} = \mathbf{y} - \mathbf{X} \boldsymbol{\beta} \in \mathcal{C}(\mathbf{X})^\perp$ is orthogonal to any vectors in $\mathcal{C}(\mathbf{X})$ including the columns of $\mathbf{X}$. Thus $$ \mathbf{X}' (\mathbf{y} - \mathbf{X} \boldsymbol{\beta}) = \mathbf{0}, $$ or equivalently, $$ \mathbf{X}' \mathbf{X} \boldsymbol{\beta} = \mathbf{X}' \mathbf{y}. $$
Proof of 2: If $\mathbf{X}$ has full column rank, $\mathbf{X}' \mathbf{X}$ is non-singular and the solution to the normal equation is uniquely determined by $\boldsymbol{\beta} = (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}' \mathbf{y}$, and the orthogonal projection is $\mathbf{u} = \mathbf{X} \boldsymbol{\beta} = \mathbf{X} (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}' \mathbf{y}$.
Example: HW5 Q1.3.
Uniqueness of orthogonal projector. Let $\mathbf{A}, \mathbf{B} \in \mathbb{R}^{n \times p}$, both of full column rank and $\mathcal{C}(\mathbf{A}) = \mathcal{C}(\mathbf{B})$. Then $\mathbf{P}_{\mathbf{A}} = \mathbf{P}_{\mathbf{B}}$.
Proof: Since $\mathcal{C}(\mathbf{A}) = \mathcal{C}(\mathbf{B})$, there exists a non-singular $\mathbf{C} \in \mathbb{R}^{p \times p}$ such that $\mathbf{A} = \mathbf{B} \mathbf{C}$. Then \begin{eqnarray*} \mathbf{P}_{\mathbf{A}} &=& \mathbf{A} (\mathbf{A}' \mathbf{A})^{-1} \mathbf{A}' \\ &=& \mathbf{B} \mathbf{C} (\mathbf{C}' \mathbf{B}' \mathbf{B} \mathbf{C})^{-1} \mathbf{C}' \mathbf{B}' \\ &=& \mathbf{B} \mathbf{C} \mathbf{C}^{-1} (\mathbf{B}' \mathbf{B})^{-1} (\mathbf{C}')^{-1} \mathbf{C}' \mathbf{B}' \\ &=& \mathbf{B} (\mathbf{B}' \mathbf{B})^{-1} \mathbf{B}' \\ &=& \mathbf{P}_{\mathbf{B}}. \end{eqnarray*}
Let $\mathbf{P}_\mathbf{X}$ be the orthogonal projector into $\mathcal{C}(\mathbf{X})$, where $\mathbf{X} \in \mathbb{R}^{n \times p}$ has full column rank. Following statements are true.
- $\mathbf{P}_\mathbf{X}$ and $\mathbf{I} - \mathbf{P}_\mathbf{X}$ are both symmetric and idemponent.
- $\mathbf{P}_\mathbf{X} \mathbf{X} = \mathbf{X}$ and $(\mathbf{I} - \mathbf{P}_\mathbf{X}) \mathbf{X} = \mathbf{O}$.
- $\mathcal{C}(\mathbf{X}) = \mathcal{C}(\mathbf{P}_\mathbf{X})$ and $\text{rank}(\mathbf{P}_\mathbf{X}) = \text{rank}(\mathbf{X}) = p$.
- $\mathcal{C}(\mathbf{I} - \mathbf{P}_\mathbf{X}) = \mathcal{N}(\mathbf{X}') = \mathcal{C}(\mathbf{X})^\perp$.
$\mathbf{I} - \mathbf{P}_\mathbf{X}$ is the orthogonal projector into $\mathcal{N}(\mathbf{X}')$ (or $\mathcal{C}(\mathbf{X})^\perp)$.
Proof of 1: Check directly using $\mathbf{P}_{\mathbf{X}} = \mathbf{X} (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}'$.
Proof of 2: Check directly using $\mathbf{P}_{\mathbf{X}} = \mathbf{X} (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}'$.
Proof of 3: Since $\mathbf{P}_{\mathbf{X}} = \mathbf{X} (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}'$, $$ \mathcal{C}(\mathbf{P}_\mathbf{X}) \subseteq \mathcal{C}(\mathbf{X}) = \mathcal{C}(\mathbf{P}_\mathbf{X} \mathbf{X}) \subseteq \mathcal{C}(\mathbf{P}_\mathbf{X}). $$
Proof of 4 (optional): The second equality is simply the fundamental theorem of linear algebra. For the first equality, first we show $\mathcal{C}(\mathbf{I} - \mathbf{P}_\mathbf{X}) \subseteq \mathcal{N}(\mathbf{X}')$: \begin{eqnarray*} & & \mathbf{u} \in \mathcal{C}(\mathbf{I} - \mathbf{P}_\mathbf{X}) \\ &\Rightarrow& \mathbf{u} = (\mathbf{I} - \mathbf{P}_\mathbf{X}) \mathbf{v} \text{ for some } \mathbf{v} \\ &\Rightarrow& \mathbf{X}' \mathbf{u} = [(\mathbf{I} - \mathbf{P}_\mathbf{X}) \mathbf{X}]' \mathbf{v} = \mathbf{O} \mathbf{v} = \mathbf{0} \\ &\Rightarrow& \mathbf{u} \in \mathcal{N}(\mathbf{X}'). \end{eqnarray*} To show the other direction $\mathcal{C}(\mathbf{I} - \mathbf{P}_\mathbf{X}) \supseteq \mathcal{N}(\mathbf{X}')$, \begin{eqnarray*} & & \mathbf{u} \in \mathcal{N}(\mathbf{X}') \\ &\Rightarrow& \mathbf{X}' \mathbf{u} = \mathbf{0} \\ &\Rightarrow& \mathbf{P}_\mathbf{X} \mathbf{u} = \mathbf{X} (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}' \mathbf{u} = \mathbf{0} \\ &\Rightarrow& \mathbf{u} = \mathbf{u} - \mathbf{P}_\mathbf{X} \mathbf{u} = (\mathbf{I} - \mathbf{P}_\mathbf{X}) \mathbf{u} \\ &\Rightarrow& \mathbf{u} \in \mathcal{C}(\mathbf{I} - \mathbf{P}_\mathbf{X}). \end{eqnarray*}
Proof of 5: For any $\mathbf{y} \in \mathbb{R}^n$, write $\mathbf{y} = \mathbf{P}_\mathbf{X} \mathbf{y} + (\mathbf{I} - \mathbf{P}_\mathbf{X}) \mathbf{y}$.
Let $\mathbf{P} \in \mathbb{R}^{n \times n}$ be symmetric with rank $r$ and $\mathbf{P} = \mathbf{U} \mathbf{U}'$ be a rank factorization of $\mathbf{P}$. Then $\mathbf{P}$ is an orthogonal projector in $\mathcal{C}(\mathbf{U})$ if and only if $\mathbf{U}' \mathbf{U} = \mathbf{I}_r$.
Above result gives another way to construct an orthogonal projector into $\mathcal{C}(\mathbf{A})$, where $\mathbf{A}$ might not be full column rank. Obtain an orthornormal basis $\mathbf{Q} \in \mathbb{R}^{n \times r}$ of $\mathcal{C}(\mathbf{A})$, e.g., by Gram-Schmidt, and let $\mathbf{P} = \mathbf{Q} \mathbf{Q}'$.
Example: HW5 Q1.3, Q7.